Updated March 23, 2023

Introduction to Transpose Matrix Matlab
In this article, we will learn about Transpose Matrix Matlab. If output matrix rows are equal to input columns and output matrix columns are equal to rows of the input matrix then the output matrix is called ‘transpose of the matrix’. This ‘T’ represents the transpose of the matrix. Let us consider there are two matrices one is the input matrix ‘I’ and the second is the output matrix ‘O’. A number of rows of the input matrix are ‘Irow’. The number of columns in the input matrix is ‘Idol’ and the number of rows in the output matrix is ‘Orow’. Number of columns in output matrix is ‘Ocol’ then Transpose of matrix satisfies two conditions which are Icol=Orow and Irow=Ocol.(rows of input matrix =column of output matrix and columns of input matrix=rows of output matrix)
How We Can Do Transpose Matrix in Matlab?
There are two ways to find out transpose of a matrix in Matlab which are:
- By Using Operator
- By Using Command
1. By Using Operator
In this method, the dot operator is used to finding the transpose of the matrix (. ’). This is one of the easiest and simple methods for transpose. The only limit of this method is there are high chances of syntax error because of the operator.
Syntax:
Output matrix=input matrix . ’
Steps:
- Accept input matrix by using square matrix (Input = [ 23 , 32 , 11 ; 22 3 2 ; 16 39 21 ; 32 4 1 ]
- Apply the operator on the input matrix ( output matrix=input matrix.’)
- Display the output matrix.
2. By Using Command
In this method, ‘transpose’ command is used to find out the transpose of the matrix. This method is less complex and easy to implement as compared to the previous method. And there are fewer chances of error at the time of implementation.
Syntax:
Output matrix=transpose (input matrix)
Steps:
- Accept input matrix by using square matrix (Input = [ 23 , 32 , 11 ; 22 3 2 ; 16 39 21 ; 32 4 1 ]
- Apply command on input matrix ( output matrix = transpose (input matrix))
- Display output matrix.
Examples for Transpose Matrix Matlab
Following are the examples implement the matrix Matlab:
Example #1
Let us consider the input matrix as mat1;
Code:
mat1 =
23 32 11
22 3 2
16 39 21
32 4 1
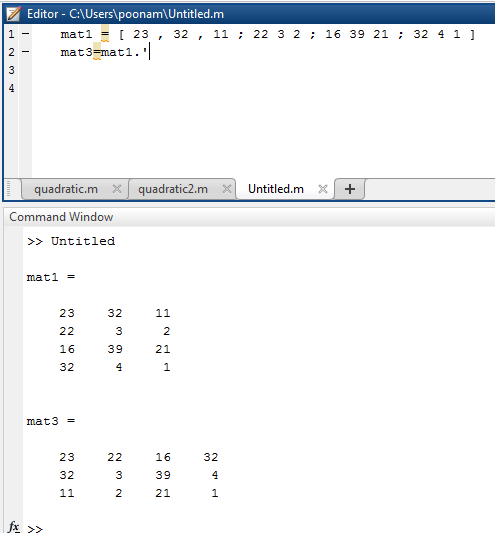
The following table illustrates the Matlab code for example 1 by using the operator.
| Matlab Editor | Command Window(output) |
|
mat1 = [ 23 , 32 , 11 ; 22 3 2 ; 16 39 21 ; 32 4 1 ] mat3 = mat1 . ‘ |
mat1 = 23 32 11 22 3 2 16 39 21 32 4 1 mat3 = 23 22 16 32 32 3 39 4 11 2 21 1 |
Output:
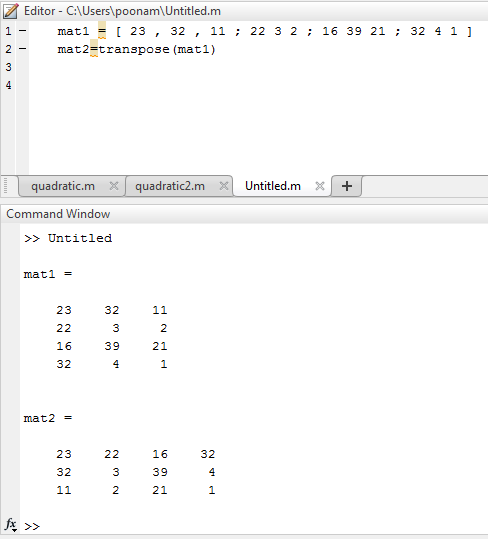
The following table illustrate the Matlab code for example 1 by using transpose command:
| Matlab Editor | Command Window(output) |
| mat1 = [ 23 , 32 , 11 ; 22 3 2 ; 16 39 21 ; 32 4 1 ]
mat2=transpose(mat1) |
mat1 = 23 32 11 22 3 2 16 39 21 32 4 1 mat2 = 23 22 16 32 32 3 39 4 11 2 21 1 |
Example #2
Let us assume input matrix is mat1 in form of the magic command.
mat1 =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
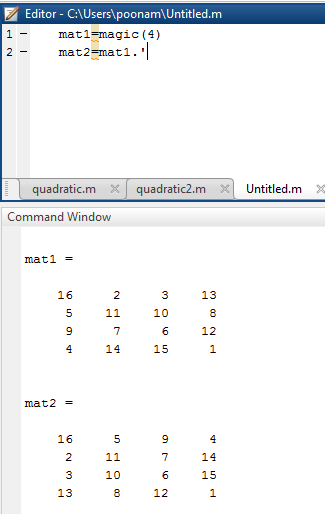
The following table illustrates the Matlab code for example 1 by using a transpose operator.
| Matlab Editor | Command Window (Output) |
|
mat1 = magic(4) mat2 = mat1.’ |
mat1 = 16 2 3 13 5 11 10 8 9 7 6 12 4 14 15 1 mat2 = 16 5 9 4 2 11 7 14 3 10 6 15 13 8 12 1 |
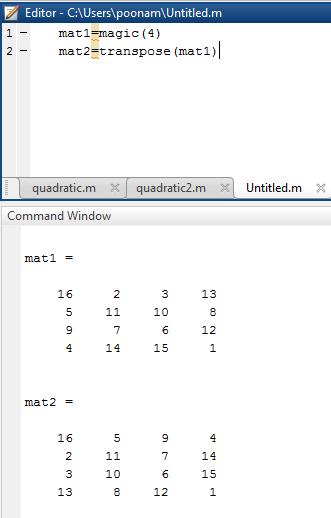
Following table illustrate the Matlab code for example 2 by using transpose command.
| Matlab Editor | Command Window ( Output ) |
| mat1 = magic ( 4 )%no 4 represents no of rows and columns%
mat2=transpose(mat1) |
mat1 =
16 2 3 13 5 11 10 8 9 7 6 12 4 14 15 1 mat2 = 16 5 9 4 2 11 7 14 3 10 6 15 13 8 12 1 |
Example #3
Now consider one input matrix with complex numbers.
mat1 =
1.0000 - 3.0000 i 4.0000 + 4.0000 i 8.0000 + 0.0000 i 2.0000 - 5.0000 i
5.0000 + 0.0000 i 3.0000 + 0.0000 i 6.0000 + 8.0000 i 4.0000 + 4.0000 i
0.0000 + 1.0000 i 7.0000 + 8.0000 i 9.0000 + 9.0000 i 10.0000 + 0.0000 i
| Matlab Editor | Command Window ( Output ) |
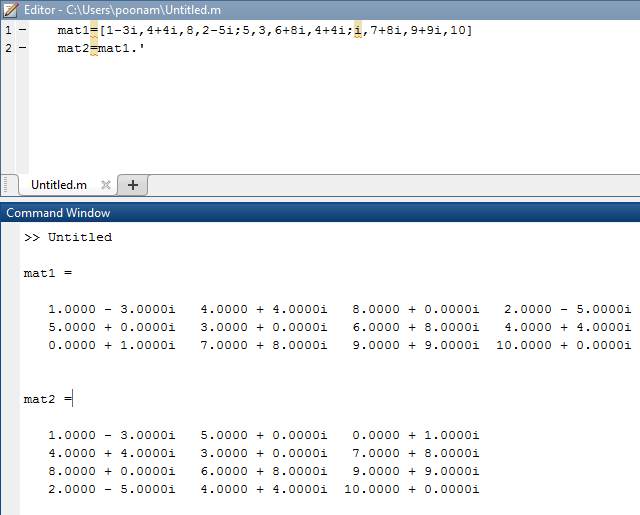
| mat1 = [ 1 – 3 i , 4 + 4 i , 8 , 2 – 5 i ; 5 , 3 , 6 + 8 i , 4 + 4 i ; i , 7 + 8 i , 9 + 9 i , 10]
mat2=mat1.’ |
mat1 =
1.0000 – 3.0000i 4.0000 + 4.0000i 8.0000 + 0.0000i 2.0000 – 5.0000i 5.0000 + 0.0000i 3.0000 + 0.0000i 6.0000 + 8.0000i 4.0000 + 4.0000i 0.0000 + 1.0000i 7.0000 + 8.0000i 9.0000 + 9.0000i 10.0000 + 0.0000i mat2 = 1.0000 – 3.0000i 5.0000 + 0.0000i 0.0000 + 1.0000i 4.0000 + 4.0000i 3.0000 + 0.0000i 7.0000 + 8.0000i 8.0000 + 0.0000i 6.0000 + 8.0000i 9.0000 + 9.0000i 2.0000 – 5.0000i 4.0000 + 4.0000i 10.0000 + 0.0000i |
| Matlab Editor | Command Window ( Output ) |
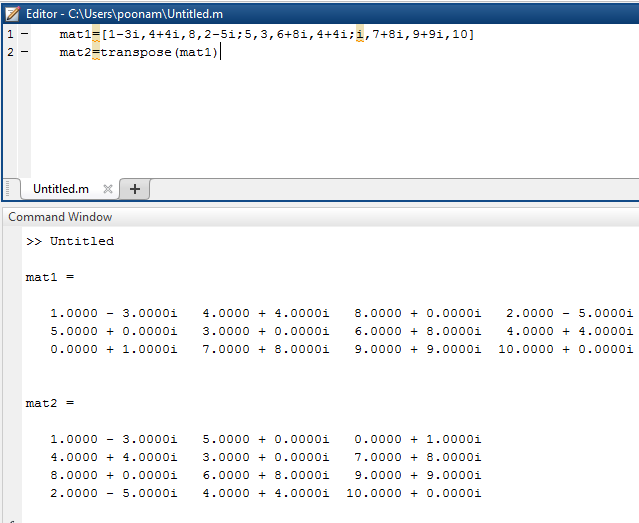
| mat1=[1-3i,4+4i,8,2-5i;5,3,6+8i,4+4i;i,7+8i,9+9i,10]
mat2=transpose(mat1) |
mat1 =
1.0000 – 3.0000i 4.0000 + 4.0000i 8.0000 + 0.0000i 2.0000 – 5.0000i 5.0000 + 0.0000i 3.0000 + 0.0000i 6.0000 + 8.0000i 4.0000 + 4.0000i 0.0000 + 1.0000i 7.0000 + 8.0000i 9.0000 + 9.0000i 10.0000 + 0.0000i mat2 = 1.0000 – 3.0000i 5.0000 + 0.0000i 0.0000 + 1.0000i 4.0000 + 4.0000i 3.0000 + 0.0000i 7.0000 + 8.0000i 8.0000 + 0.0000i 6.0000 + 8.0000i 9.0000 + 9.0000i 2.0000 – 5.0000i 4.0000 + 4.0000i 10.0000 + 0.0000i |
Conclusion
Transpose of the matrix is one of the important terminologies used in matrix manipulations. In this section we have seen how to find out transpose of a matrix by using two methods one is by using the operator and the other one is by using transpose command. Along with the different methods, we have seen different matrices as input to check the system (real numbers, random numbers, and complex numbers).
Recommended Articles
This is a guide to Transpose Matrix Matlab. Here we discuss the examples to implement the transpose matrix Matlab by using operator and command. You can also go through our other related articles to learn more –