Updated April 11, 2023
Definition of Python Tree Traversal
Python tree traversal is defined asan algorithm that is implemented in Python programming language and enables developers to develop application that requires every element to be visited as a part of the execution. Traversing means visiting and tree is an abstract data structure implementation in various programming language. Implementation of trees is non-linear in nature in comparison to other data structures like arrays or list where the elements are present in a linear fashion. The components of a tree are root and child nodes some of which ends at that particular node and is named as leaves and the others creating more sub-trees. There are requirements of a data structure for it to be named as tree which we will discuss later in this article. Also, we would look at various type of trees traversal methods in Python in this article.
Syntax:
Declaration of class in python:
def<class name> :
# Perform the required steps as a part of the classIf loop in python:
if < condition 1 > :
# Steps to be taken if the condition 1 is true
elif< condition 2 >:
# Steps to be taken if the condition 2 is true
else:
# Steps to be taken if the If condition is not satisfiedDeclaring the init function in a class
class < class name >:
def __init__(self, < variable >):
self. = < Value 1 >
self. = < Value 2 >
self. = < Value 3 >How to Perform Tree Traversal in Python?
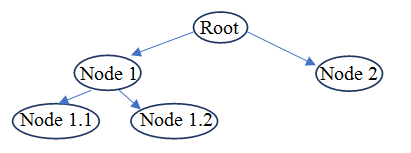
Now, we would need to first understand the structure of a tree so that when we talk about the traversal it will ensure that we understand the details of it through a visual appeal of the structure of a tree and get a better grasping of the different ways of tree traversal. In the introduction we understood that trees are a structure where there is one root node and that node gives way to child nodes and each child nodes can either be terminating there or form more sub trees. Now a traversal means that each of the nodes in the tree has to be visited and the traversal may arise if one would need to find for example, the maximum or minimum in a tree-based data structure. There are other use cases as well like finding the sum of all elements in the tree and so on. To achieve the task assigned, each of the node in the tree needs to be visited and required operations needs to be performed as per the use case. The structure of the tree is as follows:
In the above structure the root is the place where the tree formation starts and Node 1 leads to further sub trees but node 2 stops there itself. Now there are lot of condition of a data structure to be called as tree. Few of them are, there should one and only one root, the next being that one child node can’t have connection to more than one parent node, another one being one node can’t have itself as the child node.
Keeping the above pointers in mind, we have 3 types of traversals that can be implemented for a tree data structure and definition of each along with the way of traversal is listed below:
- In-order Traversal: In this method it is the left node which is visited first and then the base, or the sub node is traversed and finally at the end the right sub-tree.The pseudocode is as follows:
- The left sub tree is visited first till the node is reached.
- When the current location is the root of the sub node, the right sub tree is traversed.
- On completion of the left-sided tree traversal, we follow the same process till we reach the root node of the tree and repeat the process till all nodes are visited.
The path as per the example of the structure is: Node 1.1→Node 1→Node 1.2→Root→Node 2.
- Pre-order Traversal:In this method it is the root node which is visited first and then the left sub-tree is traversed and finally at the end the right sub-tree.The pseudocode is as follows:
- The root is the first location to visit.
- Then it moves to the left of the branch and keeps going till it encounters the end of the tree.
- Once there it starts looking at the right side of the level before elevating at the upper node level.
The path as per the example of the structure is: Root→Node 1→Node 1.1→Node 1.2→Node 2.
- Post-order Traversal:In this method it is the left side is visited first and then the right-side sub-tree is traversed and finally at the node.The pseudocode is as follows:
- The first location is the left most leaf node.
- Then it moves to the right node before moving to the upper level of node and follow the same traversal till it reaches the base node of the tree.
The path as per the example of the structure is: Node 1.1→Node 1.2→ Node 1→Node 2→ Root.
Examples of Tree Traversal Python
Examples of tree traversal python are given below:
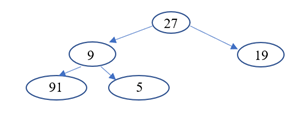
Tree for examples:
Example #1 – In order traversal
Code:
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def inOrderFunc(baseRoot):
cur = baseRoot
data = []
done = 0
while True:
if cur is not None:
data.append(cur)
cur = cur.left
elif(data):
cur = data.pop()
print(cur.data, end="→")
cur = cur.right
else:
break
print()
baseRoot = Node(27)
baseRoot.left = Node(9)
baseRoot.right = Node(19)
baseRoot.left.left = Node(91)
baseRoot.left.right = Node(5)
inOrderFunc(baseRoot)Output:
Example #2 – Pre-order traversal
Code:
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def PreOrderFunc(root):
if root is None:
return
data = []
data.append(root)
while(len(data) > 0):
node = data.pop()
print (node.data, end="→")
if node.right is not None:
data.append(node.right)
if node.left is not None:
data.append(node.left)
baseRoot = Node(27)
baseRoot.left = Node(9)
baseRoot.right = Node(19)
baseRoot.left.left = Node(91)
baseRoot.left.right = Node(5)
PreOrderFunc(baseRoot)Output:
Example #3 – Post order traversal
Code:
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def check(data):
if len(data) > 0:
return data[-1]
return None
def postOrderFunc(base):
if base is None:
return
data = []
while(True):
while (base):
if base.right is not None:
data.append(base.right)
data.append(base)
base = base.left
base = data.pop()
if (base.right is not None and
check(data) == base.right):
data.pop()
data.append(base)
base = base.right
else:
print (base.data, end="→")
base = None
if (len(data) <= 0):
break
baseRoot = Node(27)
baseRoot.left = Node(9)
baseRoot.right = Node(19)
baseRoot.left.left = Node(91)
baseRoot.left.right = Node(5)
postOrderFunc(baseRoot)Output:
Conclusion
In this article looked at the different ways of tree traversal at its easiest option. There might be other ways to achieve the same and readers are encouraged to experiment with the same as one is already clear on the basic of the 3 ways of tree traversal!
Recommended Articles
We hope that this EDUCBA information on “Tree Traversal Python” was beneficial to you. You can view EDUCBA’s recommended articles for more information.